小学校の算数や、中学高校の数学でいろいろ習いましたが、そこで習った言葉や公式や定理について、英語でなんて言うんだろうと思ったことありませんか?
そんな、算数や数学で出てくる英語をまとめてみました。
とは言っても筆者も数学から離れて長いので、あまり数学的に厳密な定義や言い方ができていないかもしれません。また、一応中学から高校レベルまでの数学について解説しますが、一部、高校レベルを超えた数学も含むことがあります。あくまで、「この言葉は英語ではこう言う」ということを意識していただければと思います。
今回は「確率・統計」編です。最近では「数学I・A」という科目になってるらしいです。
Contents
データ
データは、単数形が datum、複数形が data です。 なので The data are available. のようにいいますが、集合名詞として扱って、The data is available. といってもかまいません。
データには、定性的 (qualitative) なものと定量的 (quantitative) なものがあり、前者は何かの特性を説明するだけのもの、後者は数字を使って説明しているものになります。定量的な数字には、離散的 (discrete) なものと連続的 (continuous) なものに分けられ、前者はある特定の数字を示すもの(数えられるもの)、後者はある範囲の中でどの値をもとりうるもの(測れるもの)のことをいいます。
例えば犬について説明するとき、「毛が長い」とか「茶色」とかいうのが定性的なデータ、「足が4本ある」とか「きょうだいが2匹いる」とかいうのが定量的で離散的なデータ、「体重が25.5kg」「体長が565mm」とかいうのが定量的で連続的なデータになります。
データを集める
データを集める (collect) には、調査 (survey) をします。あるグループについて、そのメンバー全員のデータを集めることを全数調査 (census) といいます。それに対し、あるグループについて、その中から選んだメンバーだけのデータを集めることを標本調査 (sample) といいます。
標本 (sample) を選ぶことを抽出 (sampling) といいます。抽出のしかたには、無作為抽出法 (random sampling) 、系統抽出法 (systematic sampling) 、層化抽出法 (stratified sampling) 、クラスター抽出法 (cluster sampling) があります。
無作為抽出法 (random sampling) は、完全にランダムに標本を抽出するもので、一番良い抽出の方法ですが、たとえば人口調査をしようとするときに、無作為抽出をするためには、その全人口のリストを持っている必要があり、現実的でないことが多いです。
系統抽出法 (systematic sampling) とは、「10人おきに1人選ぶ」のように、ある規則にのっとって標本を選ぶ方法のことです。
層化抽出法 (stratified sampling) とは、ある特性(年齢層、性別、職業など)にもとづいてグループに分け、その比率に応じて標本を選ぶ方法のことです。たとえば、ある町の人口の7%が教師であることがわかっているとき、その町の100人に調査をするときには教師である人を7人選ぶ、というようなやり方です。
クラスター抽出法 (cluster sampling) とは、全体を多数のグループに分け、そのグループをランダムに選んだあと、選んだグループの全員について調査をする方法です。
標本を抽出したら、その標本について測定し (measure) ます。測定値 (measured value) の真の値 (true value) への近さのことをaccuracyといいます。何度か測定を行った測定値どうしの近さのことをprecisionといいます。たとえば、測定値が真の値とかけ離れていても、かたまって存在しているならば、accuracyは低いがprecisionが高いといえます。逆に測定値が真の値に近くても、ばらついているときは、accuracyは高いがprecisionが低いといえます。

accurateとpreciseのイメージの仕方としては
aCcurateのCはCorrectのC(正しい場所に当たる)
pReciseのRはRepeatingのR(同じところに何度も当たるが正しい場所とは限らない)
といったところでしょうか。
日本語では、「JIS Z 8101 統計−用語及び記号」ではaccuracyを正確度、precisionを精度といったり、「JIS Z 8103 計測用語」ではaccuracyを精度、precisionを精密度といったりして、一定しません。
また、測定値が近いところにかたまっていても、偏り (bias) があれば、それらは誤った値になります。偏りとは、常に一定量だけ誤ってしまう誤差のことで、たとえば、はかりに何も載せない状態で1キログラムをさすような場合、それで物をはかると常に1キログラム増えた状態の値をさすような誤りが出ます。このときの1キログラムのことを偏りといいます。
データを評価する
偽陽性 (false positive) と偽陰性 (false negative)
偽陽性 (false positive) とは、実際にはしていないのに、したと判断されることです。偽陰性 (false negative) とは、実際にはしたのに、していないと判断されることです。
たとえば、空港の保安検査で、鍵やコインなどの普通の物が武器と間違われ、ブザーが鳴るような場合は、「偽陽性」です。品質管理の場面では、良品が不合格になるのが「偽陽性」、不良品が合格になるのが「偽陰性」です(欠陥があることを陽性というとき)。アンチウイルスソフトで、普通のファイルをウイルスありと判断するのは「偽陽性」です。定期検診のように大人数で行う低コストの検査は、多くの偽陽性(病気でないのに病気だと言う)を出すことで、より正確な検査を受けるように仕向けたりします。
データを表示する
データは、グラフ (graph) の形で表示することがよくあります。グラフにはいろいろな種類があります。
棒グラフ (bar graph)
棒グラフ (bar graph) は、下のグラフのように、それぞれの項目の量を棒の高さで示したグラフで、相対的な大きさを示すのに非常に適しています。どのジャンルの映画が最も好まれ、どのジャンルの映画が最も好まれていないかが、一目でわかります。

円グラフ (pie chart)
円グラフ (pie chart) は、下のグラフのように、全体を1つの円であらわし、それぞれの項目の量がそのうちのどれだけの比率を占めるか、パイを切り分けるように、おうぎ形の大きさで示したグラフで、これも相対的な大きさを示すのに非常に適しています。円グラフの形でも、どのジャンルの映画が最も好まれ、どのジャンルの映画が最も好まれていないかが、一目でわかります。

折れ線グラフ (line graph)
折れ線グラフ (line graph) は、下のグラフのように、時間とともに変化する量などを線でつなげて描いたものです。

散布図 (scatter plot)
散布図 (scatter plot) とは、2種類の変数が関係性をもつ、つまり二変量である (bivariate) データについて、その関係を示すグラフです。それに対し、1種類の変数だけのデータは単変量である (univariate) といいます。
たとえば下の表は、気温とアイスクリームの売り上げの関係をあらわしています。
| Ice Cream Sales vs Temperature | |
| Temperature °C | Ice Cream Sales |
| 14.2 | $215 |
| 16.4 | $325 |
| 11.9 | $185 |
| 15.2 | $332 |
| 18.5 | $406 |
| 22.1 | $522 |
| 19.4 | $412 |
| 25.1 | $614 |
| 23.4 | $544 |
| 18.1 | $421 |
| 22.6 | $445 |
| 17.2 | $408 |
これを散布図にすると

こんな感じになります。
さらに、

このように、すべての点に最も近くなるように散布図の上に直線を引くことがあります。これを回帰直線 (regression line) あるいは趨勢線 (trend line) といい、これより上にくる点と下にくる点の数が同じになるように引きます。この線を決めるのに、最小自乗法 (least squares regression) が使われることがあります。
この線を使うと、データとして取っていない、たとえば気温21度の場合のおおよその売り上げを推定することができます。またデータの範囲外の、たとえば気温29度の場合のおおよその売り上げも、この直線を右上にのばしていけば推定することができます。前者の推定を内挿 (interpolation)、後者の推定を外挿 (extrapolation) といいます。
2種類のデータの関係が右肩上がり、あるいは右肩下がりになるとき、これらは相関 (correlation) が高いといいます。相関は \(-1\) から \(1\) までの範囲であらわされ、\(1\) に近いほど、片方が増えるともう片方も増える関係になり、 \(-1\) に近いほど、片方が増えるともう片方は減っていく関係になり、 \(0\) に近いほど両者はてんでばらばらの関係になります。
相関の値のことを相関係数 (correlation coefficient) といいます。ちなみに上の気温とアイスクリームの売り上げの関係の相関係数を求めるには、このようにします。気温を \(x\) 度、アイスクリームの売り上げを \(y\) ドルとして、次のようにします。
- \(x\) と \(y\) の平均値を求める。
- それぞれの \(x\) の値と \(x\) の平均値との差 \(a\) と、それぞれの \(y\) の値と \(y\) の平均値との差 \(b\) を求める。
- それぞれの値について、 \(ab\)、 \(a^2\)、 \(b^2\) を計算する。
- \(ab\)、 \(a^2\)、 \(b^2\) をそれぞれ合計する。
- \(ab\)の合計を、 \(a^2\) の合計と \(b^2\) の合計の積の平方根で割る。
エクセルを使うと、

このような作業になります。そして、
\[ \frac{5,325}{\sqrt{177.0\times 174,757}} = 0.9575 \]
が相関係数となります。一般に、 \(x\) と \(y\) の相関係数 \(r_{xy}\) は、
\[ r_{xy} = \frac{\sum\limits_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^n(x_i-\bar{x})^2\sum\limits_{i=1}^n(y_i-\bar{y})^2}} \]
であらわされます( \(\bar{x}, \bar{y}\) :\(x, y\) の平均値)。これをピアソンの相関係数 (Pearson correlation coefficient) ともいいます。
N.B. プログラマー向けに。 \(a\) や \(b\) を求めなくても、 \(x, y, x^2, y^2, xy\) を足し合わせるだけで相関係数を求めることができます。つまり
\[ r_{xy} = \frac{n\sum\limits_{i=1}^nx_iy_i-\sum\limits_{i=1}^nx_i\sum\limits_{i=1}^ny_i}{\sqrt{n\sum\limits_{i=1}^nx_i^2-\left(\sum\limits_{i=1}^nx_i\right)^2}\sqrt{n\sum\limits_{i=1}^ny_i^2-\left(\sum\limits_{i=1}^ny_i\right)^2}} \]
でもOKです。
ヒストグラム (histogram)
ヒストグラム (histogram) は、棒グラフとよく似ていますが、数を範囲でグルーピングします。それぞれの棒の高さは、その数の範囲内にどれだけの数あてはまるかを示します。
例として、毎月、子犬が体重がどれだけ増えたかを記録し、その結果が \(\{0.5, 0.5, 0.3, −0.2, 1.6, 0, 0.1, 0.1, 0.6, 0.4\}\) だったとしたとき、体重の増え方の範囲を \(0.5\) きざみでグルーピングし、-0.5〜0だった月の数、0〜0.5だった月の数、0.5〜1.0だった月の数、・・・をとっていき、下のようなグラフにあらわすことができます。
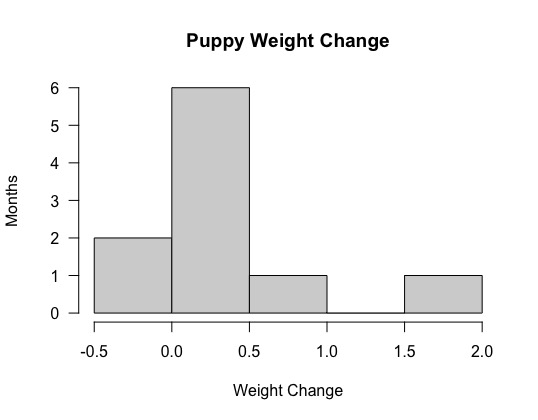
ヒストグラムは、横軸が体重、身長、時間のような連続量をとるような場合に有効です。横軸が連続的なデータではなく、カテゴリー(国名や、好きな映画のジャンルなど)になるような時は、ヒストグラムではなく棒グラフを使います。
ヒストグラムの棒の数のことをビン (bins) といいます。上のグラフのビンは5本、ビンの幅は\(0.5\)になります。
箱ひげ図 (box and whisker plot)
箱ひげ図 (box and whisker plot) とは、下の図のように、統計量を箱状の形と、その両端からのびるひげ状の線分であらわした図です。

箱の真ん中の線が中央値 (median)、箱の左端が第1四分位数 (lower quartile)、箱の右端が第3四分位数 (upper quartile) を示します。箱の左右に伸びているひげの左端が最小値 (minimum)、右端が最大値 (maximum) を示します。これらの値については後述します。
度数分布 (frequency distribution)
度数 (frequency) とは、あることがらが何回起こるかの回数をあらわします。たとえば、ある人が野球に土曜日の朝、土曜日の昼、木曜日の昼に行ったとしたら、その度数は、
土曜日:\(2\)
木曜日:\(1\)
週全体:\(3\)
ということができます。
それぞれのことがらの度数を数えて、度数分布表 (frequency distribution table) を作ることができます。
たとえば、最近の14試合であげた得点が \( \{2, 3, 1, 2, 1, 3, 2, 3, 4, 5, 4, 2, 2, 3\} \) だったとしたとき、
| Score | Frequency |
|---|---|
| 1 | 2 |
| 2 | 5 |
| 3 | 4 |
| 4 | 2 |
| 5 | 1 |
のような、得点と度数の関係の表になります。
幹葉図 (stem and leaf plot)
幹葉図 (stem and leaf plot) とは、データ値を幹 (stem) と葉 (leaf) に分けて表にしたものです。
たとえば、\( \{15, 16, 21, 23, 23, 26, 26, 30, 32, 41 \} \) という一覧があったとき、一番目の数字 \(15\) なら、幹を一桁目の数字である \(1\)、葉を二桁目の数字である \(5\) に分け、三番目の数字 \(21\) なら、幹を \(2\)、葉を \(1\) に分け、・・・という作業をして、
| Stem | Leaf |
|---|---|
| 1 | 5 6 |
| 2 | 1 3 3 6 6 |
| 3 | 0 2 |
| 4 | 1 |
のような表になります。
累積 (cumulative)
たとえば、3月に$120、4月に$50、5月に$110稼いだとします。
このとき、3月の累積合計 (cumulative total) は
| Month | Earned | Cumulative |
|---|---|---|
| March | $120 | $120 |
のような表になります。4月の累積合計は
| Month | Earned | Cumulative |
|---|---|---|
| March | $120 | $120 |
| April | $50 | $170 |
5月の累積合計は
| Month | Earned | Cumulative |
|---|---|---|
| March | $120 | $120 |
| April | $50 | $170 |
| May | $110 | $280 |
のようになります。
統計
平均値 (mean)
2つの値の平均値 (mean) は、それぞれの値の中間の部分の値になります。例えば、\(3\) と \(7\) があったとき、その平均値は \(5\) になります。
3つ以上の値の平均値は、その値を全部たし合わせ、それを値の数で割ったものになります。
平均値は必ずしもそのグループの特質をきちんと説明できるとは限りません。たとえば、年齢13歳の子どもが6人、1歳の幼児が5人いたとすると、その平均値は \((13\times 6+1\times 5)\div 11 = 7.5...\) となり、平均年齢7.5歳ということになりますが、そもそも13歳と1歳しかいないグループでこのような平均年齢を出しても意味がありませんね。
そういうときは、中央値を使います。
中央値 (median)
中央値 (median) とは、数値を大きい順あるいは小さい順にならべたとき、真ん中にくる数値をいいます。
上記の年齢13歳の子ども6人、1歳の幼児5人のグループの場合、それを小さい順にならべると、
\[ \{1, 1, 1, 1, 1, 13, 13, 13, 13, 13, 13\} \]
となるので、ちょうど真ん中の値は \(13\)、つまり中央値13歳ということになります。
偶数個の数値の場合、真ん中の値が2つあることになります。たとえば \( \{3, 4, 7, 9, 12, 15\} \) の真ん中の数は \(7\) と \(9\) なので、中央値はその2つの数値の平均値、つまり \((7+9)\div 2 = 16\div 2 = 8\) になります。
最頻値 (mode)
最頻値 (mode) とは、もっとも頻繁にあらわれる数値のことをいいます。
上記の年齢13歳の子ども6人、1歳の幼児5人のグループの場合、13が6回、1が5回出てきているので、最頻値は13歳ということになります。
最頻値が2つある場合、そのような性質のことを二峰性 (bimodal) といいます。最頻値が3つ以上あることを多峰性 (multimodal) といいます。
外れ値 (outlier)
他の値と極端にかけ離れた値があるとき、その値のことを外れ値 (outlier) といいます。このような値は平均値を狂わせるので、統計処理から除外するか、中央値や最頻値を代わりに使います。
たとえば5人のグループがいて、年収がそれぞれ300万円、400万円、400万円、500万円、1億400万円としたとき、このまま平均値を求めると \((300+400+400+500+10400)\div 5 = \) 2400万円となりますが、5人中4人が300万円〜500万円しか年収がないのに、平均年収2400万円といわれても、ピンときませんよね。
このようなときは、外れ値 \(10400\) を除いて \( (300+400+400+500)\div 4 = \) 400万円とするか、中央値・最頻値(いずれも400万円になる)を使います。
重みづけ平均値 (weighted mean)
\( \{1, 2, 3, 4\}\) の平均値は、\((1+2+3+4)\div 4=2.5\) であらわされますが、これは見方を変えると
\[ \frac{1}{4}\times 1 + \frac{1}{4}\times 2 + \frac{1}{4}\times 3 + \frac{1}{4}\times 4 \\= 0.25 + 0.5 + 0.75 + 1 = 2.5 \]
とあらわすこともできます。言い換えると、\( \{1, 2, 3, 4\}\) のそれぞれに \(1/4\) という重み (weight) をつけているということもできます。
これに、たとえば \(3\) の重みを \(0.7\) 、他の3つの重みを \(0.1\) というふうに(重みの和が1になるように)変えて足し算してみると
\[ 0.1\times 1 + 0.1\times 2 + 0.7\times 3 + 0.1\times 4 \\= 0.1+0.2+2.1+0.4 = 2.8 \]
となります。このように重みを変えて平均値を取ったものを重みづけ平均値 (weighted mean) と言います。この場合、3の重みに引っ張られて、平均値よりも大きい数字になっています。
重みづけ平均値は、たとえば、上司が部下に任務を3つ与え、任務1は重要なので50%、任務2はそこそこ重要なので30%、任務3はあまり重要でないので20%の重みをつけて、それぞれの任務に5段階評価をつけて、任務1については4点、任務2については3点、任務3は5点、というふうに人事評価するとしたとき、総合評価はこれらの重みづけ平均値 \( 0.50\times 4+0.30\times 3 + 0.20\times 5 = 2 + 0.9 + 1 = 3.9 \) 点、というふうに評価するときに使ったりします。
いろいろな平均値
足して全体の数で割る平均値のことを算術平均値 (arithmetic mean) ともいいます。平均の取り方はこのほかに、幾何平均値 (geometric mean) 、調和平均値 (harmonic mean) というのもあります。
幾何平均値とは、\( \{x_1, x_2, ..., x_n\}\) に対して、
\[ \sqrt[n]{x_1x_2\cdots x_n}\]
のように、数値を \(n\) 個かけ合わせたものの \(n\) 乗根 (\(n\)-th root) であらわしたものです。
調和平均値とは、
\[ \frac{n}{\frac{1}{x_1}+\frac{1}{x_2}+\cdots +\frac{1}{x_n}} \]
のように、逆数 (reciprocal) の算術平均値の逆数をとったものです。
四分位数 (quartile)
数の一覧を昇順に並べ、その一覧を4等分したとき、その分割点にくる数のことを四分位数 (quartile) といいます。
たとえば、\( 5, 7, 4, 4, 6, 2, 8 \) があったとき、これを昇順に並べると \(2, 4, 4, 5, 6, 7, 8 \)
これを4等分すると、
 この7つの数の四分位数は2番目の \(4\) 、4番目の \(5\) 、6番目の \(7\) になり、順に第1四分位数 (Quartile 1 (Q1) lower quartile) 、第2四分位数 (Quartile 2 (Q2) middle quartile) 、第3四分位数 (Quartile 3 (Q3) upper quartile) といいます。第2四分位数のことを中央値 (median) ともいいます。
この7つの数の四分位数は2番目の \(4\) 、4番目の \(5\) 、6番目の \(7\) になり、順に第1四分位数 (Quartile 1 (Q1) lower quartile) 、第2四分位数 (Quartile 2 (Q2) middle quartile) 、第3四分位数 (Quartile 3 (Q3) upper quartile) といいます。第2四分位数のことを中央値 (median) ともいいます。

上図のように、数が偶数個あるときは、第2四分位数は、真ん中の2つの数字の平均値になります。
四分位範囲 (IQR: interquartile range) とは、第3四分位数と第1四分位数の差 (difference) で定義されます。\(2, 4, 4, 5, 6, 7, 8 \) のIQRは \(7-4=3\)、\(1, 3, 3, 4, 5, 6, 6, 7, 8, 8\) のIQRは \(7-3=4\) となります。
パーセンタイル (percentile)
昇順に並べたとき、最小のものから全体の80%のところの位置の値を80パーセンタイル (80th percentile) のようにいいます。50パーセンタイルのことを中央値 (median) ともいいます。第一四分位数は25パーセンタイル (25th percentile)、第三四分位数は75パーセンタイル (75th percentile) となります。
十分位数 (decile)
10パーセンタイルのことを十分位数 (decile) といいます。第1十分位数 (1st decile) とは10パーセンタイルのことで、その数より少ない数が全体の10%になるようなところの数のことです。第2十分位数 (2nd decile) とは20パーセンタイルのことで、その数より少ない数が全体の20%になるようなところの数のことです。第5十分位数 (5th decile) のことを中央値 (median) ともいいます。
四分位数、パーセンタイル、十分位数の関係を下図に示します。背の順に左から並ぶとき、それぞれの値はこのようになります。

平均偏差 (mean deviation)
\(\{3, 6, 6, 7, 8, 11, 15, 16\}\) という数の一覧があったとき、これの平均値 (mean) は
\[(3+6+6+7+8+11+15+16)\div 8 \\ =72\div 8=9\]
です。それぞれの数の、平均値からの離れぐあい、つまり偏差 (deviation) は、平均値との差であらわされ、
\[\{9-3, 9-6, 9-6, 9-7, 9-8, 11-9, 15-9, 16-9\} \\ =\{6, 3, 3, 2, 1, 2, 6, 7\}\]
です。この差のことを絶対偏差 (absolute deviation) といい、その平均値
\[ (6+3+3+2+1+2+6+7)\div 8 = 30\div 8 = 3.75\]
のことを平均偏差 (mean deviation) といいます。平均値を \(\mu\) 、数の総数を \(N\) 、それぞれの数を \(x\) とすると、平均偏差は
\[\frac{\sum\limits_{i=1}^N|x_i-\mu|}{N} \]
とあらわされます。
分散 (variance)
分散 (variance) は、偏差の自乗平均
\[ \frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2 \]
で定義されます。ここで \(x_i\) はそれぞれの数値、 \(\mu\) は平均値、\(N\) は数値の数となります。
上記の式は母集団 (population) から数値全部をひろってきた統計量となります。このような標準偏差のことを母分散 (population variance) ともいいます。
そうではなく、母集団から標本を抽出して、その標本の分散を求めることにより母集団の分散を推定することがあります。標本だけの分散のことを標本分散 (sample variance) といい、
\[ \frac{1}{N-1}\sum\limits_{i=1}^N(x_i-\bar{x})^2 \]
であらわされます。ここで \(\bar{x}\) は標本平均値 (sample mean) 、\(N\) は標本の数となります。
標準偏差 (standard deviation)
標準偏差 (standard deviation) とは、分散の平方根をとったものです。
標準偏差の公式は
\[ \sqrt{\frac{1}{N}\sum_{i=1}^N(x_i-\mu)^2} \]
となります。これは母集団から数値全部をひろってきたもので、母標準偏差 (population standard deviation) ともいいます。
標本分散の平方根、つまり標本だけの標準偏差のことを標本標準偏差 (sample standard deviation) といい、
\[ \sqrt{\frac{1}{N-1}\sum_{i=1}^N(x_i-\bar{x})^2} \]
であらわされます。ここで \(\bar{x}\) は標本平均値、\(N\) は標本の数となります。
標本分散や標本標準偏差と、母分散や母標準偏差との違いは、 \(N\) で割り算するところを \(N-1\) で割り算するところです。これをベッセルの修正 (Bessel's correction) といいます。
共分散 (covariance)
\(x\) と \(y\) の共分散 (covariance) \(\mathrm{Co v}(x,y)\) とは、\(x\) と \(y\) のそれぞれの偏差の積の平均値
\[ \mathrm{Co v}(x,y) = \frac{1}{N}\sum\limits_{i=1}^N\left(x_i-\bar{x}\right)\left(y_i-\bar{y}\right) \]
であらわされます。
さて、 \(x\) と \(y\) の相関係数 \(r_{xy}\) は
\[ r_{xy} = \frac{\sum\limits_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum\limits_{i=1}^N(x_i-\bar{x})^2\sum\limits_{i=1}^N(y_i-\bar{y})^2}} \]
であらわされることを上のほうで紹介しましたが、この分母と分子をそれぞれ \(N\) で割ると
\[ \begin{eqnarray} r_{xy} & = & \frac{\frac{1}{N}\sum\limits_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})}{\frac{1}{N}\sqrt{\sum\limits_{i=1}^N(x_i-\bar{x})^2\sum\limits_{i=1}^N(y_i-\bar{y})^2}} \nonumber \\ & = & \frac{\frac{1}{N}\sum\limits_{i=1}^N(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\frac{1}{N}\sum\limits_{i=1}^N(x_i-\bar{x})^2}\sqrt{\frac{1}{N}\sum\limits_{i=1}^N(y_i-\bar{y})^2}} \end{eqnarray} \]
となります。つまり、 \(x\) と \(y\) の相関係数 \(r_{xy}\) は、 \(x\) と \(y\) の共分散を \(x\) の標準偏差と \(y\) の標準偏差の積で割ったものとして求められるということになります。
実習
「英語で数学〜確率・統計(2)〜」に続きます。