英語で数学〜数と式（２）〜

小学校の算数や、中学高校の数学でいろいろ習いましたが、そこで習った言葉や公式や定理について、英語でなんて言うんだろうと思ったことありませんか？

そんな、算数や数学で出てくる英語をまとめてみました。

英語で数学〜数と式（１）〜はこちらをご覧ください。

Contents

数列 (sequence) と級数 (series)

数列 (sequence)

数列 (sequence) とは、

\[\{1, 4, 9, 16, 25, 36, ...\}\]

や

\[\{1, 1, 2, 3, 5, 8, 13, 21, ...\}\]

のように、あるパターンに 従った一続きの数たちのことです。

数列 \(\{a_1, a_2, a_3, ...\}\) のそれぞれの \(a_n\) のことをその数列の項 (term) といいます。前者の数列は

\[a_n=a^n\]

後者はフィボナッチ数 (Fibonacci number) といい、

\[a_n=a_{n-1}+a_{n-2}\]

のように一般にあらわされます。

\(\{0, 3, 6, 9, 12, ...\}\) や \(\{10, 5, 0, −5, −10, ...\}\) のように、項と項の間の差 (difference) が同じになる数列を等差数列あるいは算術数列 (arithmetic sequence) といいます。前者の数列を一般的な式であらわすと

\[a_n=3n-3\]

後者の数列は

\[a_n=10-5(n-1) = -5n+15\]

となります。

\[\{3, 6, 12, 24, ...\}\]

や

\[\left\{\frac{3}{2}, -\frac{1}{3}, \frac{2}{27}, -\frac{4}{243}, ...\right\}\]

のように、項にある比率 (ratio) を掛け算して次の項にしていくような数列のことを等比数列あるいは幾何数列 (geometric sequence) といいます。前者は

\[ a_n = 3 \times 2^{n-1}\]

後者は

\[ a_n = \frac{3}{2}\left(-\frac{2}{9}\right)^{n-1} \]

です。

級数 (series)

数列の和 (sum) のことを級数 (series) といいます。級数はギリシャ文字の\(\sum\)をつかってあらわすのが一般的です。

等差数列の和のことを等差級数または算術級数 (arithmetic series) といいます。

数学者 Carl Friedrich Gauss (1777-1855) という人はその昔、９歳の頃、 \(1 + 2 + 3 + \cdots + 99 + 100\) まで順に足していったらどうなるか、その答えを導き出して大いに驚かれたといいます。その種明かしは、一番端っこの\(1\)と\(100\)を足すと\(101\)、１つ内側の\(2\)と\(99\)を足すとこれも\(101\)、そのまた内側の\(3\)と\(98\)を足してもこれも\(101\)、\(\cdots\)というふうに、足して\(101\)になるペアが\(50\)組あることに着目し、 \(101 × 50 = 5050\) と計算したのでした。

このように、一般に、\(1\)から\(n\)までの足し算は、足して\(n + 1\)になるペアが\(\frac{n}{2} \)個あることになります。つまり等差級数

\[ \sum_{k=1}^nk = 1+2+\cdots +(n-1)+n \\ = (n+1)\left(\frac{n}{2}\right) \\ = \frac{n(n+1)}{2} \]

となります。

等比数列の和を等比級数あるいは幾何級数 (geometric series) といいます。一般に、等比数列 \( \{a_1, a_1r, a_1r^2, a_1r^3, ... \} \) の和

\[ \sum_{i=1}^na_1r^{i-1} =  a_1\frac{1-r^n}{1-r} \cdots\cdots (1) \]

になります。これを証明する (prove) のに、まず \(n = 1\) の場合について考えます。

\[ \sum_{i=1}^1a_1r^{i-1} = a_1\frac{1-r^1}{1-r} = a_1 \]

なので、 \(n = 1\) の場合について \( (1)\) の式が成り立ちます。次に、 \(n = k\) のときに

\[ \sum_{i=1}^ka_1r^{i-1} = a_1\frac{1-r^k}{1-r} \]

が真 (true) だと仮定したとき、 \(n = k + 1\) のときもそれが真かどうかをみます。

\[ \begin{eqnarray}   \sum_{i=1}^{k+1}a_1r^{i-1} &=& a_1\frac{1-r^k}{1-r}+a_1r^{(k+1)-1} \nonumber \\      &=&   a_1\frac{1-r^k}{1-r}+a_1r^k \nonumber \\      &=&   a_1\left(\frac{1-r^k}{1-r}+r^k\right) \nonumber \\      &=& a_1\left\{\frac{1-r^k}{1-r}+\frac{(1-r)r^k}{1-r}\right\} \nonumber \\      &=& a_1\frac{1-r^k+r^k-r^{k+1}}{1-r} \nonumber \\      &=& a_1\frac{1-r^{k+1}}{1-r} \nonumber \end{eqnarray} \] 

となるので、 \(n = k + 1\) でも真であることがわかります。 \(n = 1\) のとき真で、 \(n = k\) のときに真と仮定したものが \(n = k + 1\) でも真の場合、すべての場合について真であることが証明できます。このようなやり方を数学的帰納法 (mathematic induction) といいます。

集合 (set)

数の集まりのことを集合 (set) といいます。上記の数列 \(\{1, 4, 9, 16, 25, 36, ...\}\) や \(\{1, 1, 2, 3, 5, 8, 13, 21, ...\}\) や、\(12\)の約数の集まり \(\{1, 2, 3, 4, 6, 12\}\) なども集合の一種です。集合は、\(\{1, 2, 3, 4\}\) や、 \(\{2, -3, 4, -5, 6\}\) のように、中かっこ (set brackets あるいは braces) でくくってあらわします。

集合を構成する１つ１つのことを集合の要素 (element) あるいは元 (member) といいます。要素同士はコンマで区切ってあらわします。

要素が無限に続くときは、\(\{3, 6, 9, ...\}\) のように、ドット３つ (ellipsis) であらわします。

集合\(A\)が \(A=\{1, 2, 3\}\) であるとき、\(1\)は集合\(A\)の要素であり、\(1\in A \)のようにあらわします。また\(5\)は集合\(A\)の要素ではないので、 \(5\notin A\) のようにあらわします。

要素のない集合のことを空集合 (empty set) といい、\(\emptyset\) であらわします。

２つの集合 \(A = \{1, 2, 3, 4, 5, 6\}\) 、 \(B = \{4, 6, 8, 10\}\) があったとき、その少なくともどちらかに属している元の集合、この場合だと \(\{1, 2, 3, 4, 5, 6, 8, 10\}\) のことを\(A\)と\(B\)の和集合 (union) といい、\(A\cup B\) のようにあらわします。集合\(A\)、\(B\)のどちらにも属している元の集合、この場合だと \(\{4, 6\}\) のことを \(A\) と \(B\) の共通部分 (intersection) といい、\(A\cap B\) のようにあらわします。

\(A\cap B = \emptyset\) であるとき、 \(A\) と \(B\) は互いに素である (mutually disjoint) といいます。

\(A-B = \{1, 2, 3, 5\}\) のことを集合の差 (difference) といい、\(A\)の元のうちから\(B\)の元となるものを取り除いた集合になります。

さてそうしたときにあらためて関数というものを考えてみると、関数とは、集合\(A\)の元から集合\(B\)の元へマッチングさせる方法のことということもできます。集合\(A\)の１つの元から集合\(B\)の複数の元をさすようなものは関数とはいいません。ただし\(A\)の複数の元から\(B\)の同じ元をさすことはあります。

関数 \(y=f(x)\) について、独立変数 (independent variable) \(x\) の範囲のことを定義域 (domain) といいます。それに対して、対応する従属変数 (dependent variable) \(y\) の範囲のことを値域 (range) と言います。

集合 \(A\) の複数の元が集合\(B\)の同じ元をさすことがない関係を単射 (injective)といいます。 \(B\) のすべての元が \(A\) の少なくとも１つの元からさし示される関係を全射 (surjective) といいます。全単射 (bijective) とは、単射でありかつ全射である関係のことです。つまり \(A\) の元も \(B\) の元もすべて相手がおり、孤立した元がない状態になります。全単射の関数には逆関数が存在します。

三角関数 (trigonometric function)

三角関数 (trigonometric function) の基本は余弦 (cosine) 、正弦 (sine) 、正接 (tangent) で、それぞれ \(\cos\theta\) 、\(\sin\theta\)、\(\tan\theta\) のように書きます。\(\theta\) は度 (degree) やラジアン (radian) であらわします。

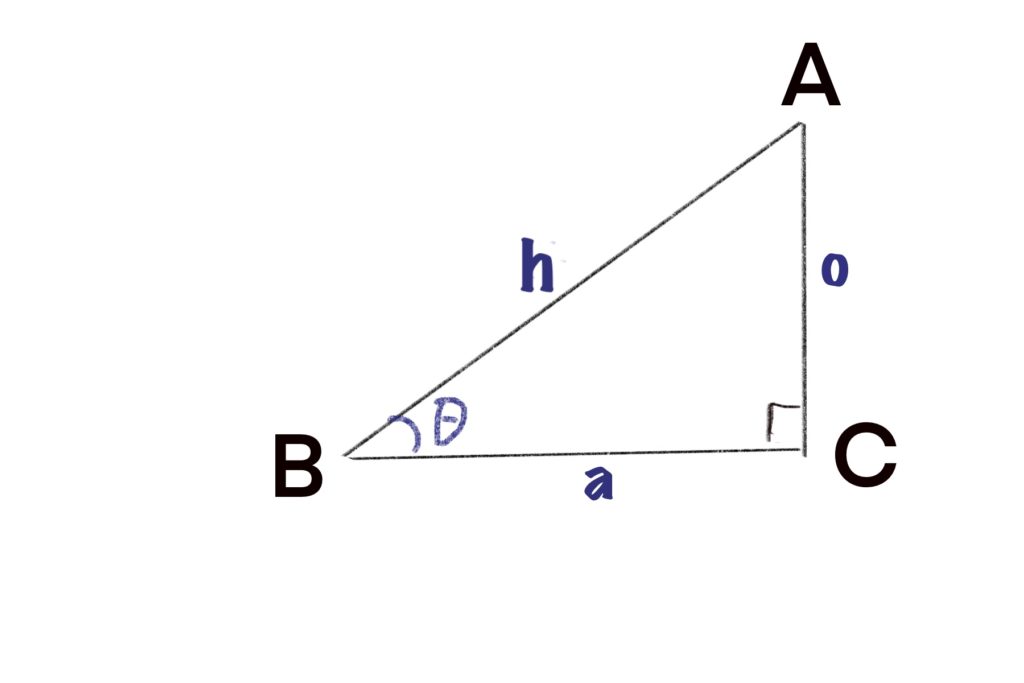
直角三角形 (right triangle) \(\triangle\) ABC において、角 (angle) \(\angle\)ACB が直角 (rectangle) とするとき、辺 (side) ABのことを斜辺 (hypotenuse) といいます。\(\angle\)ABCの角度を\(\theta\)とし、辺ABの長さを \(h\)、\(\angle\)ABCの対辺 (opposite side) ACの長さを\(o\)、辺BCの長さを\(a\)とすると、

\[ \begin{eqnarray} \cos\theta & = & \frac{a}{h} \\ \sin\theta & = & \frac{o}{h} \\ \tan\theta & = & \frac{o}{a} \end{eqnarray} \]

となります。

\(\cos\theta\)、\(\sin\theta\)、\(\tan\theta\) の逆数 (reciprocal) をそれぞれ正割 (secant) 、余割 (cosecant) 、余接 (cotangent) といい、それぞれ \(\mathrm{se c}\theta\)、\(\mathrm{cs c}\theta\)、\(\mathrm{co t}\theta\) と書きます。つまり

\[ \mathrm{se c}\theta = \frac{1}{\cos\theta} \\ \mathrm{cs c}\theta = \frac{1}{\sin\theta} \\ \mathrm{co t}\theta = \frac{1}{\tan\theta} \]

です。

\[  \begin{eqnarray} \sin\theta & = & \pm \sqrt{1 - \cos^2\theta} \nonumber \\ \tan\theta & = & \frac{\sin\theta}{\cos\theta} \nonumber \\            & = & \pm\frac{\sqrt{1-\cos^2\theta}}{\cos\theta} \nonumber \\ \mathrm{se c}\theta & = & \frac{1}{\cos\theta} \nonumber \\ \mathrm{cs c}\theta & = & \frac{1}{\sin\theta} \nonumber \\            & = & \pm\frac{1}{\sqrt{1-\cos^2\theta}} \nonumber \\            & = & \pm\frac{\sqrt{1-\cos^2\theta}}{1-\cos^2\theta} \nonumber \\ \mathrm{co t}\theta & = & \frac{1}{\tan\theta} \nonumber \\            & = & \pm\frac{\cos\theta}{\sqrt{1-\cos^2\theta}} \nonumber \\            & = & \pm\frac{\cos\theta}{1-\cos^2\theta}\sqrt{1-\cos^2\theta} \nonumber \end{eqnarray} \]

となるので、すべての三角関数は\(\cos\)だけで書きあらわすことができます。

\( x=\cos\theta \)、\( x=\sin\theta \)、\( x=\tan\theta \) の逆関数 (inverse function) はそれぞれ \(\theta=\mathrm{a rcsi n} x\)、\(\theta = \mathrm{ar cc os} x\)、\(\theta = \mathrm{ar ct an} x\) と書きます。

双曲線関数

双曲線余弦関数 (hyperbolic cosine) 、双曲線正弦関数 (hyperbolic sine) は、以下のようにあらわされます。

\[ \mathrm{co sh} x = \frac{e^x+e^{-x}}{2} \\ \mathrm{si nh} x = \frac{e^x-e^{-x}}{2} \]

双曲線正接関数 (hyperbolic tangent) は、

\[ \mathrm{ta nh} x = \frac{\mathrm{si nh} x}{\mathrm{co sh} x} = \frac{e^x-e^{-x}}{e^x+e^{-x}} \]

であらわされます。

\(\mathrm{co sh} x\)、\(\mathrm{si nh} x\)、\(\mathrm{ta nh} x\) の逆数 (reciprocal) をそれぞれ双曲線正割関数 (hyperbolic secant) 、双曲線余割関数 (hyperbolic cosecant) 、双曲線余接関数 (hyperbolic cotangent) といい、それぞれ \(\mathrm{se ch} x\)、\(\mathrm{cs ch} x\)、\(\mathrm{co th} x \) と書きます。

極限値 (limit)・微分 (differentiation)・積分 (integration)

関数 \(f(x)=\frac{1}{x}\) について、変数 \(x\) を無限大 (infinity) に近づけていくと \(0\) に収束し (converge) ます。このことを

\[ \lim_{x\to\infty}\frac{1}{x} = 0 \]

のような式であらわします。このような値を極限値 (limit) といいます。この関数を正の側、負の側から0に近づけていくと

\[ \begin{eqnarray} \lim_{x\to+0}\frac{1}{x} & = & \infty \nonumber \\ \lim_{x\to-0}\frac{1}{x} & = & -\infty \nonumber \end{eqnarray} \]

のように、それぞれ正の無限大 (positive infinity) 、負の無限大 (negative infinity) に発散し (diverge) ます。

余弦関数 (cosine function) \(f(x)=\cos x\) のような関数の場合は、常に\(+1\)と\(-1\)の間を行ったり来たりするので、\(x\)を無限大に近づけても収束も発散もしません。このように、極限値が確定しないことを振動する (oscillate) といいます。

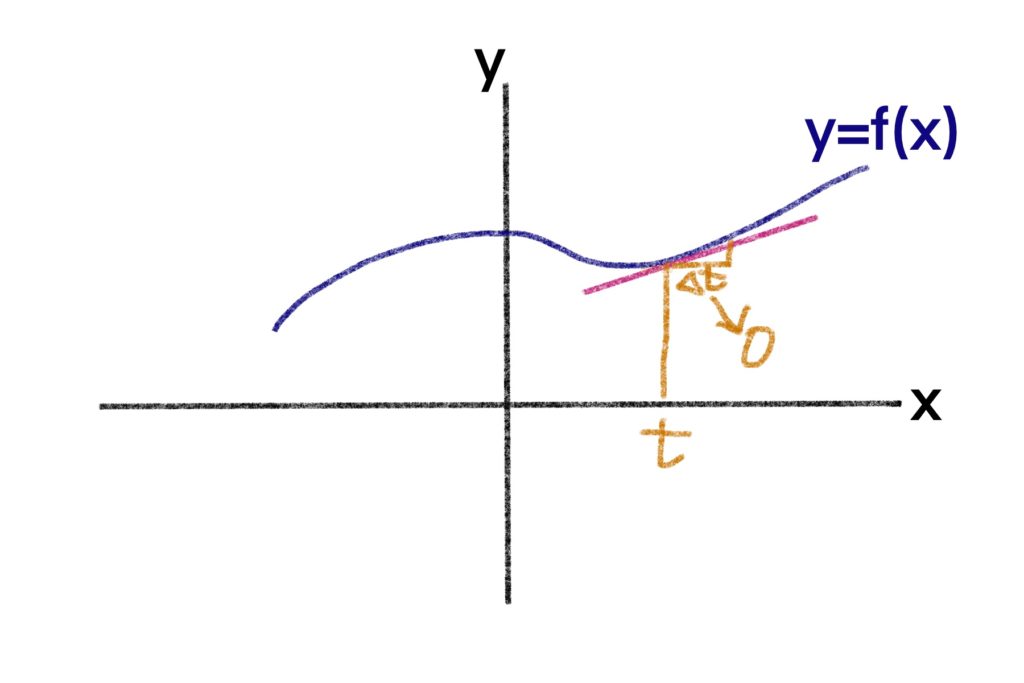
関数\(f(x)\)の、\(x=t\)における傾き (slope) をみてみましょう。\(x=t\)における傾きは、\(t\)から微小値ずれた\(t+\Delta t\)における関数\(f(t+\Delta t)\)と、\(t\)における関数\(f(t)\)との差を求め、それを\(\Delta t\)で割ったものを、\(\Delta t\)を\(0\)に近づけた極限値

\[ \lim_{\Delta t\to 0}\frac{f(t+\Delta t)-f(t)}{t+\Delta t-t} \]

として求められます。一般に、\(x\)における\(f(x)\)の傾きは

\[ \lim_{\Delta t\to 0}\frac{f(x+\Delta t)-f(x)}{\Delta t} = \frac{df(x)}{dx} \]

となります。このような\(\frac{df(x)}{dx}\)のことを関数\(f(x)\)の導関数 (derivative) といい、\(f'(x)\)であらわすこともあります。\(f(x)\)の導関数を求めることを\(f(x)\)を微分する (differentiate) あるいは\(f(x)\)の微分 (differentiation) といいます。

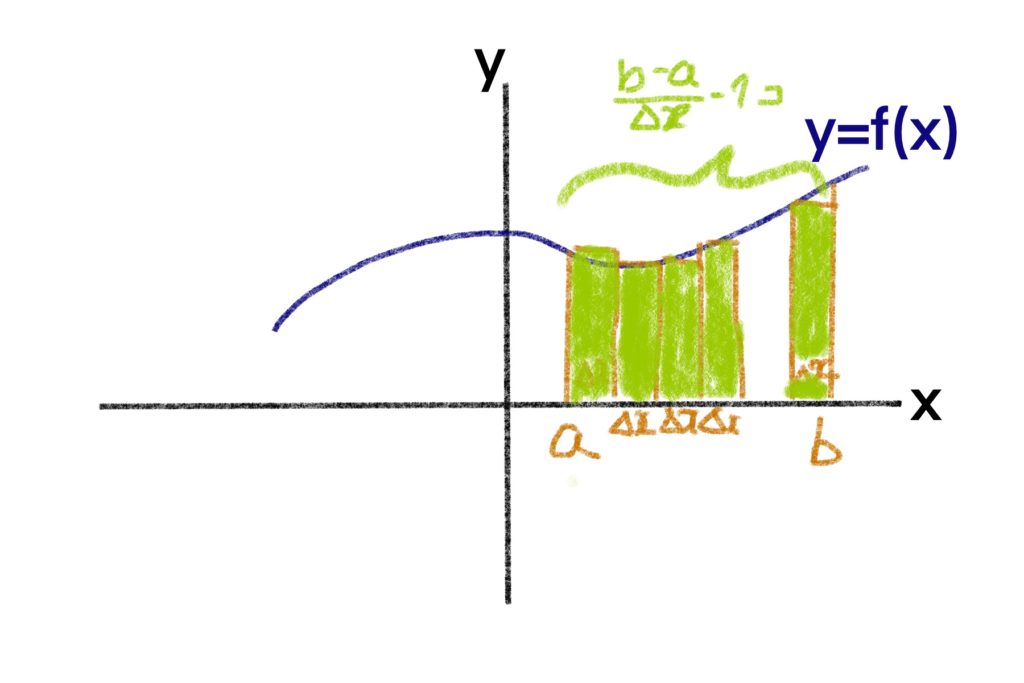
関数\(f(x)\)において、\(x=a\)のところで、辺の長さが \(\Delta x\) と\(f(a)\)との長方形を考え、その面積 (area) を求めると、\(f(a)\Delta x\)になります。次に、 \(x=a+\Delta x\) のところで、辺の長さが \(\Delta x\) と \(f(a+\Delta x)\)との長方形の面積 \(f(a+\Delta x)\Delta x\) を求めます。次に、 \(x=a+2\Delta x\) のところで、一辺の長さが \(\Delta x\) と \(f(a+2\Delta x)\) との長方形の面積 \(f(a+2\Delta x)\Delta x\) を求めます。同じようにして、\(x=b\) \( (a<b)\) のところまで、辺の長さが \(\Delta x\) と \(f(x)\) の長方形の面積を求め、足し合わせると、

\[ f(a+\Delta x)\Delta x + f(a+2\Delta x)\Delta x + f(a+3\Delta x)\Delta x \\ + \cdots + f\left( a+\left( \frac{b-a}{\Delta x}\right)\Delta x\right)\Delta x \\ = \sum_{k=1}^{\frac{b-a}{\Delta x}}f(a+k\Delta x)\Delta x \]

となります。ここで\(\Delta x\)を\(0\)に近づけると

\[ \lim_{\Delta x\to 0} \sum_{k=1}^{\frac{b-a}{\Delta x}}f(a+k\Delta x)\Delta x = \int_a^bf(x)dx \]

のように、積分記号 (integral symbol) を使ってあらわします。このように、関数 \(f(x)\) について、\(a\)から\(b\)までの区間を微小な区間に区切って、その微小区間ごとに長方形の面積を求めて足し合わせることを\(a\)から\(b\)まで積分する (integrate from \(a\) to \(b\)) といいます。このように、区間を定めて積分することを定積分 (definite integration) 、区間を定めないで積分することを不定積分 (indefinite integration) といいます。不定積分の場合は

\[ \int\frac{1}{x}dx = \ln |x| + C \]

のように、定数 \(C\) が発生します。これを積分定数 (constant of integration) といいます

関数 \(f(x_1, x_2, \cdots x_n)\) のような、複数の変数をもつ関数において、ある１つの変数（たとえば \(x_1\) ）のみに着目し、他の変数を定数とみなした状態での導関数のことを偏導関数 (partial derivative) といい、偏導関数を求めることを偏微分する (partially differentiate) あるいは名詞で偏微分 (partial differentiation) といい、 \( \frac{\partial}{\partial x_1}f(x_1, x_2, \cdots x_n) \) のようにあらわします。たとえば \( z = x^2 + y^2 + y + 3 \) を \(x\) 、\(y\) について偏微分するとそれぞれ

\[ \frac{\partial z}{\partial x} = 2x \\ \frac{\partial z}{\partial y} = 2y + 1 \]

となります。

\[ \int\int\cdots\int_Df(x_1, x_2, \cdots x_n)dx_1dx_2\cdots dx_n \]

のように、積分記号を複数使って関数 \(f(x_1, x_2, \cdots x_n)\) の積分を求めることを重積分 (multiple integral) といいます。ここで \(D\) は積分領域 (integral domain) といいます。積分記号を２個使った積分を二重積分 (double integral) 、積分記号を３個使った積分を三重積分 (triple integral) といいます。重積分は定積分だけであり、不定積分はありません。

複素数の関数（複素関数）も同様に微分、積分することができます。例えば \(z = x+iy\) （ \(x, y\) は実数、\(i\) は虚数単位）のときも関数 \(f(z)=z^2 + z + 1\) の微分は \(\frac{df(z)}{dz} = 2z+1\) になります。

複素関数 \(f(z) = u(x,y)+iv(x,y)\) について、

\[ \begin{eqnarray} \frac{\partial u}{\partial x}(x, y) & = & \frac{\partial v}{\partial y}(x, y) \\ \frac{\partial u}{\partial y}(x, y) & = & -\frac{\partial v}{\partial x}(x, y) \end{eqnarray} \]

が成り立ちます。これらをコーシー・リーマンの方程式 (Cauchy–Riemann equations) といいます。また

\[ \begin{eqnarray} \frac{\partial^2u}{\partial x^2}+\frac{\partial^2u}{\partial y^2} & = & 0 \\ \frac{\partial^2v}{\partial x^2} + \frac{\partial^2v}{\partial y^2} & = & 0 \end{eqnarray} \]

が成り立ちます。これらをラプラス方程式 (Laplace's equations) といいます。

複素関数の積分は、実数部分を横軸に、虚数部分を縦軸にとった複素平面 (complex plain) を使って考えます。実関数の積分は１次元の区間（積分区間）の中で積分しますが、複素関数の場合は複素平面の上を二次元的に経路を通って積分します。

始点から複素平面上を１周ぐるっと回って元の位置に戻る経路で積分することを周回積分 (contour integral) といい、 \( \oint_C f(z)dz\) のようにあらわします（\(C\) は積分経路）。ふつう、複素平面上を周回積分すると、積分結果は \(0\) になりますが、複素平面上のある点を囲むような経路で周回積分したときは、積分結果が \(0\) にならないことがあります。そのような点のことを特異点 (singularity) といいます。また特異点を囲む経路で周回積分した結果のことを留数 (residue) といい、\( \mathrm{Res}(f, a) \) あるいは \( \mathrm{Res}_a(f) \) とあらわします（ \(f(z)\) は複素関数、\(z=a\) は特異点）。

\[ \mathrm{Res}_a(f(z)) = \frac{1}{2\pi i}\oint_{\gamma}f(z)dz \]

と定義されます（\(\gamma\) は特異点を中心とした円の円周上の積分経路）。これを留数定理 (residue theorem) といいます。

参考

Math is Fun